Abipusis arba abipusis yra labai naudingas visų rūšių algebrinėse lygtyse. Pavyzdžiui, kai dalijate vieną trupmeną iš kitos, pirmąją trupmeną padauginate iš antrosios. Ieškodami tiesės lygties, taip pat turite naudoti atvirkštinę versiją.
Žingsnis
1 iš 3 metodas: trupmenos ar sveikojo skaičiaus atvirkštinės dalies nustatymas
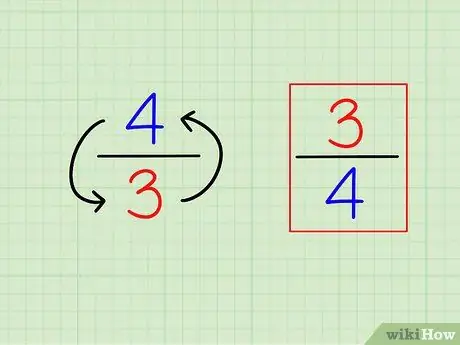
Žingsnis 1. Raskite trupmenos abipusį, apversdami ją
Apibrėžti „abipusį“arba atvirkščiai yra labai paprasta. Norėdami rasti bet kurio sveikojo skaičiaus abipusį skaičių, tiesiog apskaičiuokite „1 (tas skaičius)“. Frakcijų atveju abipusis yra kitokia trupmena, tai yra, skaičiai yra „apversti“(atvirkštiniai).
- Pavyzdžiui, priešingai 3/4 yra 4/3.
- Bet koks skaičius, padaugintas iš abipusės grąžos 1.
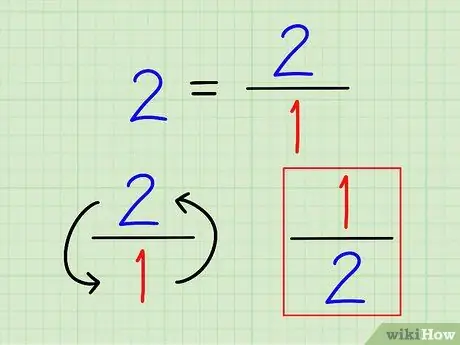
Žingsnis 2. Užrašykite viso skaičiaus abipusį skaičių kaip trupmeną
Vėlgi, skaičiaus abipusis skaičius visada yra 1 (tas skaičius). Jei yra sveikųjų skaičių, parašykite juos trupmenomis. Nėra prasmės skaičiuoti šio skaičiaus po kablelio.
Pavyzdžiui, atvirkštinis 2 yra 1 2 = 1/2.
2 metodas iš 3: mišrios dalies atvirkštinės dalies nustatymas
1 žingsnis. Nustatykite mišrius skaičius
Mišrias trupmenas sudaro sveikieji skaičiai ir trupmenos, pvz., 24/5. Yra du žingsniai, kaip rasti mišraus skaičiaus abipusiškumą, kaip aprašyta toliau.
Žingsnis 2. Paverskite mišrius skaičius į netinkamas trupmenas
Atminkite, kad 1 visada gali būti parašytas kaip (skaičius)/(tas pats skaičius), o trupmenos su tuo pačiu vardikliu (apatinis skaičius) gali būti sudedamos. Štai pavyzdys naudojant 24/5:
- 24/5
- = 1 + 1 + 4/5
- = 5/5 + 5/5 + 4/5
- = (5+5+4)/5
- = 14/5.
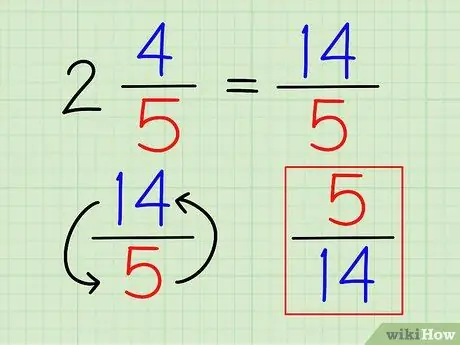
Žingsnis 3. Apverskite dalį
Kai skaičius bus visiškai parašytas kaip trupmena, atvirkštinę trupmeną galite rasti kaip ir bet kurią kitą trupmeną.
Aukščiau pateiktame pavyzdyje abipusis 14/5 yra 5/14.
3 iš 3 metodas: dešimtainio skaičiaus priešingybės radimas
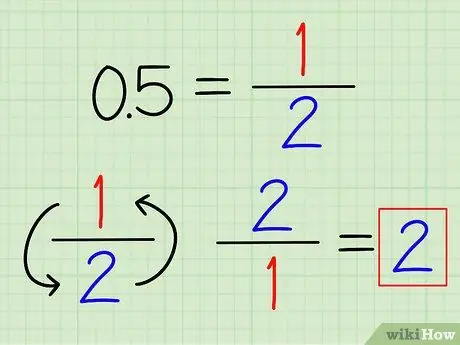
Žingsnis 1. Jei įmanoma, dešimtainius konvertuokite į trupmenas
Galite atpažinti kai kuriuos dažnai naudojamus dešimtainius skaičius, kuriuos galima lengvai paversti trupmenomis. Pavyzdžiui, 0,5 = 1/2 ir 0,25 = 1/4. Kai dešimtainis skaičius bus paverstas trupmena, tiesiog apverskite trupmeną, kad rastumėte jos abipusį skaičių.
Pavyzdžiui, abipusis 0,5 yra 2/1 = 2.
Žingsnis 2. Parašykite padalijimo problemą
Jei negalite jo konvertuoti į trupmeną, apskaičiuokite skaičiaus abipusį padalijimo uždavinio pavidalu: 1 (dešimtainis). Norėdami tai išspręsti, galite naudoti skaičiuotuvą arba pereiti prie kito veiksmo, kad išspręstumėte jį rankiniu būdu.
Pavyzdžiui, apskaičiuodami 1 0,4, galite rasti abipusį 0,4
Žingsnis 3. Pakeiskite padalijimo problemą, kad būtų naudojami sveikieji skaičiai
Pirmasis žingsnis dalijant dešimtainius yra perkelti kablelį, kol visi skaičiai yra sveikieji skaičiai. Kol perkelsite abiejų skaičių dešimtainį tašką tuo pačiu žingsnių skaičiumi, gausite teisingą atsakymą.
Pavyzdžiui, galite naudoti 1 0, 4 ir perrašyti kaip 10 4. Tokiu atveju visas dešimtaines dalis perkeliate vieną žingsnį į dešinę, taip pat padaugindami kiekvieną skaičių iš dešimties
Žingsnis 4. Išspręskite problemą naudodami ilgą padalijimą
Norėdami apskaičiuoti abipusį, naudokite ilgo padalijimo metodą. Jei suskaičiuosite 10 4, gausite atsakymą 2, 5 kuris yra abipusis 0, 4.
Patarimai
- Neigiamas skaičiaus abipusis yra toks pat kaip įprastas abipusis, nes jis dauginamas iš neigiamo. Pavyzdžiui, neigiamas abipusis 3/4 yra -4/3.
- Abipusis arba abipusis dažnai vadinamas „daugybos atvirkštiniu“.
- Skaičius 1 yra priešingas sau, nes 1 1 = 1.
- Skaičius 0 neturi abipusės reikšmės, nes 0 neapibrėžtas.
