- Autorius Jason Gerald [email protected].
- Public 2024-01-15 08:19.
- Paskutinį kartą keistas 2025-01-23 12:25.
Mechaninėje inžinerijoje pavarų santykis yra tiesioginis dviejų ar daugiau pavarų, kurie yra konkurencingai įjungti, sukimosi greičio matavimas. Paprastai taikant dvi pavaras, jei pavaros pavara (pavara, kuri sukimosi jėgą gauna tiesiogiai iš variklio, variklio ir pan.) Yra didesnė už varomą, pavara sukasi greičiau ir atvirkščiai. Šią pagrindinę sąvoką galime parašyti formule Pavarų santykis = T2/T1, T1 yra pirmosios pavaros dantų skaičius, o T2 - antrosios pavaros dantų skaičius.
Žingsnis
1 iš 2 metodas: pavarų skaičiaus apskaičiavimas pavarų grandinėje
Dvi pavaros
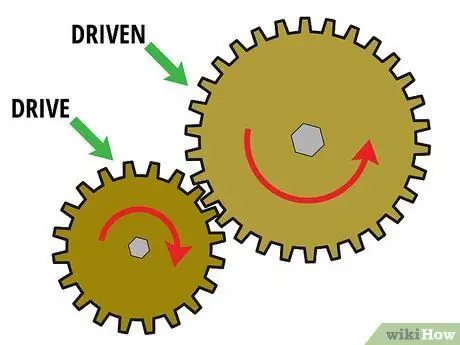
Žingsnis 1. Pradėkite nuo dviejų pavarų komplekto
Norėdami nustatyti pavarų skaičių, turite sujungti bent dvi pavaras. Šios dvi tarpusavyje sujungtos pavaros vadinamos „pavarų rinkiniais“. Paprastai pirmoji pavara yra „pavaros pavara“, sumontuota ant variklio veleno, o antroji pavara yra „varoma pavara“, sumontuota ant apkrovos veleno. Tarp pavarų taip pat gali būti keletas pavarų, perduodančių galią iš pavaros pavaros į varomą pavarą. Šios pavaros vadinamos „be apkrovos“.
Dabar pažvelkime į pavarų komplektą, kuriame yra tik dvi pavaros. Norint apskaičiuoti pavarų santykį, šios dvi pavaros turi sąveikauti viena su kita. Kitaip tariant, dantys turi būti tinkleliai, o vienas turi suktis kitu. Pavyzdžiui, tarkime, kad turite mažą pavaros pavarą (1 pavara), kuri sukasi didesnę pavarą (2 pavara)
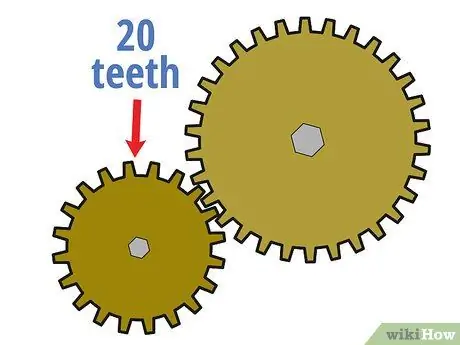
2 žingsnis. Apskaičiuokite krumpliaračio krumpliaračių skaičių
Vienas iš būdų, kaip apskaičiuoti pavarų santykį tarp dviejų tarpusavyje sujungtų pavarų, yra palyginti jų turimų dantų (mažų danties formos iškilimų ant rato krašto) skaičių. Pradėkite skaičiuoti, kiek dantų yra pavaros pavara. Tai galite padaryti skaičiuodami rankiniu būdu arba kartais žiūrėdami į pavaros pavaroje išspausdintą informaciją.
Pavyzdžiui, tarkime, kad sistemoje yra mažesnė pavaros pavara 20 dantų.
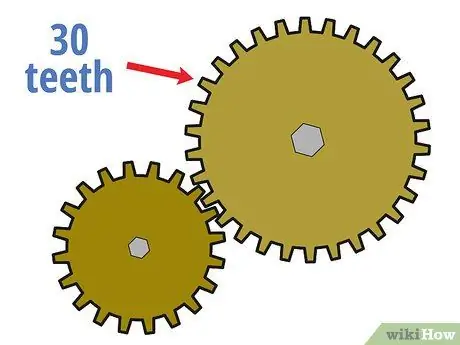
Žingsnis 3. Apskaičiuokite varomosios pavaros dantų skaičių
Tada suskaičiuokite, kiek dantų yra varomojoje pavaroje, kaip ir anksčiau.
Pavyzdžiui, tarkime, kad varomoji pavara turi 30 dantų.
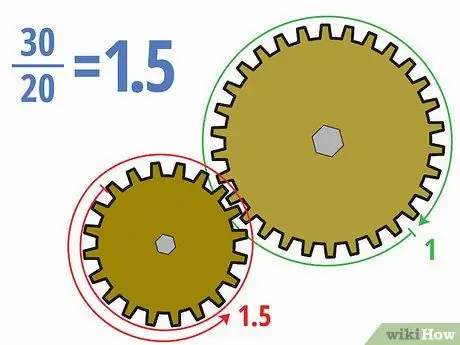
Žingsnis 4. Padalinkite dantų skaičių vienas su kitu
Dabar, kai žinote, kiek dantų yra kiekvienoje pavaroje, galite gana lengvai apskaičiuoti pavarų skaičių. Varomosios pavaros dantis padalinkite iš pavaros krumpliaračio dantų. Priklausomai nuo užduoties, atsakymą galite parašyti dešimtainiu, trupmeniniu arba santykio pavidalu (pvz., X: y).
- Pirmiau pateiktame pavyzdyje padalijus 30 dantų varomoje pavara iš 20 dantų pavaros pavara, gaunama 30/20 = 1, 5. Mes taip pat galime jį parašyti 3/2 arba 1, 5: 1.
- Šio pavarų skaičiaus reikšmė yra ta, kad mažesnė pavara turi suktis pusantro karto, kad didesnė pavara atliktų vieną pilną apsisukimą. Kadangi varoma pavara yra didesnė, varoma pavara sukasi lėčiau.
Daugiau nei dvi pavaros
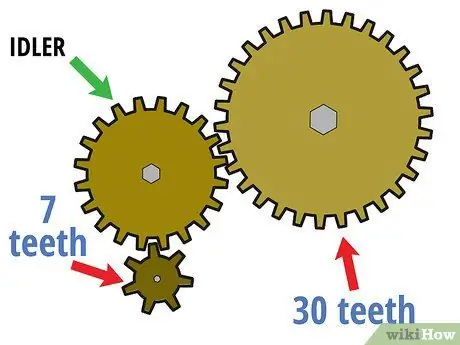
Žingsnis 1. Pradėkite nuo pavarų komplekto, kuriame yra daugiau nei dvi pavaros
Kaip rodo pavadinimas, „pavarų komplektą“gali sudaryti ilgos pavarų serijos, o ne tik viena pavara ir viena varoma pavara. Tokiu atveju pirmoji pavara išlieka varančioji, paskutinė pavara-varoma, o vidurinė-„be apkrovos“. Šios neapkrautos pavaros dažnai naudojamos sukimosi krypčiai pakeisti arba dviem pavaroms sujungti, kai dėl tiesioginio pavarų reguliavimo jos būtų sunkios arba nepasiekiamos.
Pavyzdžiui, tarkime, kad aukščiau aprašyta dviejų pavarų grandinė yra varoma pavara, turinčia septynis mažus dantis. Šiuo atveju pavara, turinti 30 fiksuotų dantų, tapo varoma pavara, o pavara, turėjusi 20 dantų (kuri anksčiau buvo pavara), dabar yra neiškrauta pavara
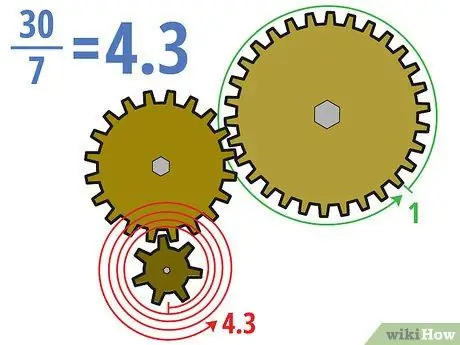
Žingsnis 2. Padalinkite pavaros ir varomosios pavaros dantų skaičių
Svarbus dalykas, kurį reikia atsiminti dirbant su reduktoriais, turinčiais daugiau nei dvi pavaras, yra tai, kad svarbu tik varančioji pavara ir varomoji pavara (dažniausiai pirmoji ir paskutinė pavara). Kitaip tariant, be apkrovos krumpliaračiai visiškai neturi įtakos viso komplekto pavarų skaičiui. Nustačius pavaros ir pavaros pavarą, galite apskaičiuoti pavarų santykį taip pat, kaip ir anksčiau.
Anksčiau pateiktame pavyzdyje mes apskaičiuosime pavaros santykį, padaliję trisdešimt varomos pavaros dantų iš septynių naujos pavaros krumpliaračio. 30/7 = apytiksliai 4, 3 (arba 4, 3: 1). Tai reiškia, kad pavaros pavara turi suktis apie 4,3 karto, kad daug didesnė varoma pavara apsisuktų vieną kartą.
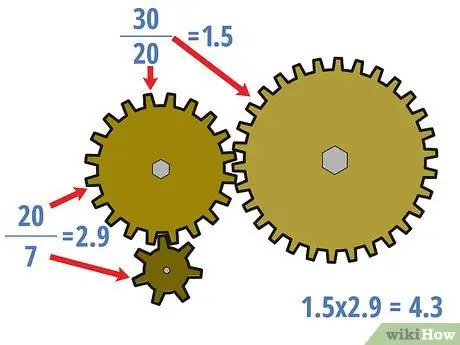
3 žingsnis. Jei reikia, apskaičiuokite centrinės pavaros pavaros santykį
Galite apskaičiuoti pavarų perdavimo skaičių, kuris taip pat apima neapkrautas pavaras, ir galbūt norėsite tai padaryti tam tikrose situacijose. Tokiu atveju pradėkite nuo varančiosios pavaros ir pereikite prie krovinio. Ankstesnę pavarą traktuokite kaip pavaros pavarą iki kitos pavaros. Padalinkite kiekvienos „varomos“pavaros dantų skaičių iš „varančiosios“pavaros krumpliaračių skaičiaus kiekvienam blokuojančių pavarų rinkiniui, kad apskaičiuotumėte centrinį pavarų skaičių.
- Aukščiau pateiktame pavyzdyje centrinis pavaros santykis yra 20/7 = 2, 9 ir 30/20 = 1, 5. Reikėtų pažymėti, kad šie santykiai nėra tokie patys kaip viso komplekto pavaros santykis, kuris yra 4,3.
- Tačiau, taip pat reikėtų pažymėti, kad (20/7) × (30/20) = 4, 3. Apskritai krumpliaračio vidurinių pavarų santykiai turėtų būti padauginti, kad būtų lygus visų pavarų santykis.
2 metodas iš 2: santykio/greičio skaičiavimai
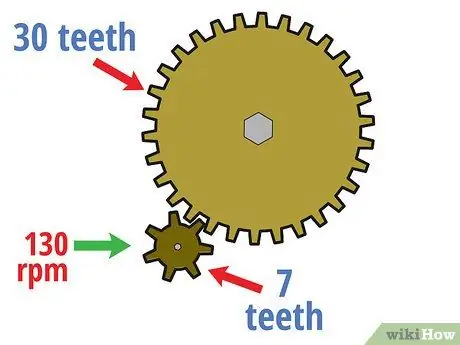
Žingsnis 1. Apskaičiuokite pavaros pavaros sukimosi greitį
Naudojant pavarų skaičiaus sąvoką, lengva nustatyti, kaip greitai sukasi varoma pavara, atsižvelgiant į pavaros pavaros „įvesties“greitį. Pradedantiesiems apskaičiuokite pavaros pavaros sukimosi greitį. Daugelio pavarų skaičiavimų rezultatas yra apsisukimai per minutę (aps./min.), Nors galima naudoti ir kitus greičio vienetus.
Pavyzdžiui, tarkime, kad aukščiau pateiktame pavarų grandinės pavyzdyje, kai pavaros pavara turi septynis dantis ir varoma pavara turi 30 dantų, pavara sukasi 130 aps./min. Turėdami šią informaciją, mes apskaičiuosime varomosios pavaros greitį atlikdami šiuos veiksmus
Žingsnis 2. Įtraukite šią informaciją į formulę S1 × T1 = S2 × T2
Šioje formulėje S1 reiškia pavaros pavaros sukimosi greitį, T1 - pavaros krumpliaračio dantis, o S2 ir T2 - pavaros pavarą. Užpildykite šiuos kintamuosius tol, kol liks tik vienas kintamasis.
- Dažnai tokiuose klausimuose rasite S2 dydį, nors galima rasti ir kitų kintamųjų. Aukščiau pateiktame pavyzdyje įvesdami turimą informaciją gausime:
- 130 aps / min × 7 = S2 × 30
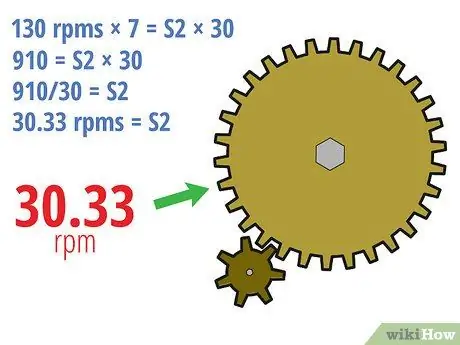
Žingsnis 3. Baigti
Likusių kintamųjų apskaičiavimas yra tik pagrindinė matematikos užduotis. Supaprastinkite likusias lygtis ir izoliuokite kintamąjį vienoje lygties ženklo pusėje ir gausite atsakymą. Nepamirškite parašyti teisingais vienetais. Dėl to galite prarasti namų darbų vertę.
- Aukščiau pateiktame pavyzdyje mes galime tai išspręsti:
- 130 aps / min × 7 = S2 × 30
- 910 = S2 × 30
- 910/30 = S2
- 30, 33 aps./min = S2
- Kitaip tariant, jei pavaros pavara sukasi 130 aps./min., Varoma pavara sukasi 30,33 aps./min. Kadangi varoma pavara yra daug didesnė, varoma pavara sukasi daug lėčiau.
Patarimai
- Norėdami pamatyti, kaip taikomas pavarų santykio principas, pabandykite važiuoti dviračiu. Atminkite, kad lengviausias būdas lipti yra tada, kai priekyje yra maža pavara, o gale - didelė pavara. Lengviau pasukti mažesnę pavarą su pedalų jėga, tačiau reikia daug apsisukti, kad galinis ratas suktųsi, palyginti su pavara, kurią naudosite lygiems paviršiams. Dėl to judate lėčiau.
- Sumažintai sistemai (kai apkrovos apsisukimų dažnis yra mažesnis nei variklio apsisukimų dažnis) reikės variklio, kuris užtikrintų optimalią galią esant didesniam sukimosi greičiui.
- Kroviniui vairuoti reikalinga galia nuo variklio pakeliama arba nuleidžiama per pavaros perdavimo skaičius. Šio variklio dydis turi būti pakeistas, kad būtų užtikrinta apkrovos reikalaujama galia, kai apskaičiuojamas pavaros santykis. Pakeltai sistemai (kai apkrovos apsisukimų dažnis yra didesnis nei variklio apsisukimų dažnis) reikės variklio, kuris užtikrina optimalią galią esant mažesniam sukimosi greičiui.






