- Autorius Jason Gerald [email protected].
- Public 2024-02-01 14:14.
- Paskutinį kartą keistas 2025-01-23 12:25.
Poslinkis fizikoje reiškia objekto padėties pasikeitimą. Kai apskaičiuojate poslinkį, jūs apskaičiuojate, kiek toli objektas yra pagal jo pradinę ir galutinę vietas. Formulė, kurią naudojate poslinkiui apskaičiuoti, priklauso nuo problemai pateikto kintamojo. Norėdami apskaičiuoti poslinkį, atlikite šiuos veiksmus.
Žingsnis
1 dalis iš 5: Rezultato poslinkio apskaičiavimas

1 žingsnis. Naudokite gautą poslinkio formulę, jei atstumo vienetas naudojamas jūsų pradžios ir pabaigos vietoms nurodyti
Nors atstumas skiriasi nuo poslinkio, dėl to kyla poslinkio problema - kiek kilometrų ar metrų objektas nuvažiavo. Naudodami šį matavimo vienetą apskaičiuosite poslinkį ir kiek objekto vieta nukrypsta nuo pradinio taško.
- Gautoji poslinkio formulė parašyta taip: S = x²+y². S yra poslinkis. X yra pirmoji objekto judėjimo kryptis, o Y - antroji objekto judėjimo kryptis. Jei jūsų objektas juda tik viena kryptimi, tada Y = 0.
- Objektas gali judėti ne daugiau kaip dviem kryptimis, nes judėjimas šiaurės/pietų arba rytų/vakarų ašimi laikomas neutraliu judesiu.

Žingsnis 2. Sujunkite taškus judėjimo tvarka ir pažymėkite juos nuo A iki Z
Naudokite liniuotę, kad nubrėžtumėte tiesią liniją iš taško į tašką.
- Taip pat nepamirškite sujungti pradžios taško su pabaigos tašku tiesia linija. Tai yra poslinkis, kurį mes apskaičiuosime.
- Pavyzdžiui, jei objektas juda į rytus 300 m ir į šiaurę 400 m, jis sudarys stačiakampį trikampį. AB bus pirmoji trikampio atkarpa, o BC - antroji. AC bus trikampio hipotenuzė, o jo dydis - objekto poslinkis. Šiame pavyzdyje dvi kryptys yra rytai ir šiaurė.

3 veiksmas. Įveskite x² ir y² reikšmes
Dabar, kai žinote dvi objekto judėjimo kryptis, įveskite reikšmes į atitinkamus kintamuosius.
Pavyzdžiui, x = 300 ir y = 400. Jūsų formulė turėtų atrodyti taip: S = 300² + 400²
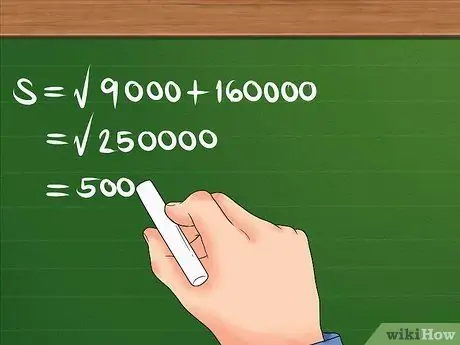
Žingsnis 4. Apskaičiuokite formulę naudodami operacijų eilę
Pirmiausia kvadratus 300 ir 400, tada sudėkite juos ir raskite sumos kvadratinę šaknį.
Pavyzdžiui: S = 90000 + 160000. S = 250000. S = 500. Dabar žinote, kad poslinkis yra 500 m
2 dalis iš 5: Kai žinomas greitis ir laikas

Žingsnis 1. Naudokite šią formulę, kai problema nurodo objekto greitį ir laiką
Kai kurios matematikos problemos nepasakys, kiek toli ar kaip greitai objektas juda. Galite apskaičiuoti poslinkį naudodami šį laiko ir greičio dydį.
-
Šiuo atveju formulė tampa tokia: S = 1/2 (u + v) t.
U = pradinis objekto greitis arba kaip greitai objektas pradeda judėti tam tikra kryptimi. V = galutinis objekto greitis arba kaip greitai objektas juda galutinės vietos link. T = laikas, per kurį objektas pasiekia galutinę vietą.
- Pavyzdys: automobilis važiuoja keliu 45 sekundes (reikalingas laikas). Automobilis sukasi į vakarus 20 m/s (pradinis greitis), o kelio pabaigoje jo greitis yra 23 m/s (galutinis greitis). Apskaičiuokite poslinkį pagal šiuos veiksnius.

Žingsnis 2. Įveskite reikiamą greitį ir laiką į atitinkamus kintamuosius
Dabar, kai žinote, kiek automobilis juda, kaip greitai automobilis juda pradžioje ir pabaigoje, galite rasti atstumą nuo pradinės vietos iki galutinės vietos.
Jūsų formulė turėtų atrodyti taip: S = 1/2 (20 + 23) 45

Žingsnis 3. Apskaičiuokite formulę, įdėję reikšmes į teisingą vietą
Nepamirškite laikytis operacijų eilės, kitaip poslinkiai sukels labai skirtingas vertes.
- Taikant šią formulę nesvarbu, ar netyčia sukeisite pradžios ir pabaigos greitį. Kadangi šiuos skaičius pirmiausia sudėsite, nesvarbu, kur jie yra skliausteliuose. Tačiau kitoms formulėms pakeitus pradinį ir galutinį greitį, bus gautos skirtingos poslinkio vertės.
- Jūsų formulė turėtų atrodyti taip: S = 1/2 (43) 45. Pirmiausia padalinkite 43 iš 2, o tai reiškia 21, 5. Tada padauginkite 21, 5 iš 45, taigi rezultatas yra 967,5 metrai. 967, 5 yra jūsų poslinkio dydis arba tai, kiek jūsų automobilis nukrypo nuo pradinio taško.
3 dalis iš 5: Kai yra žinomas pradinis greitis, pagreitis ir laikas
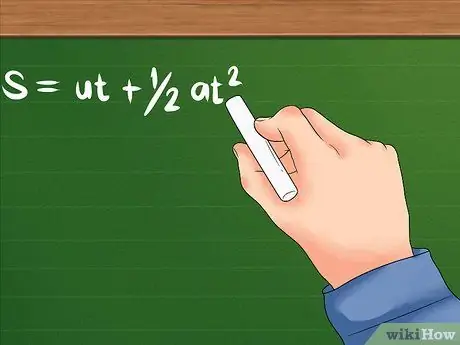
Žingsnis 1. Naudokite pakeistą formulę, kai greitis yra žinomas, be pradinio greičio ir laiko
Kai kurie klausimai tik pasakys, kaip greitai objektas juda pradžioje, kaip greitai objektas pradeda greitėti ir kiek toli juda objektas. Jums reikės šios formulės.
- Šios problemos formulė yra tokia: S = ut + 1/2at². U vis tiek rodo pradinį greitį; a yra objekto pagreitis arba kaip greitai pradeda keistis jo greitis. T gali reikšti laiką, kurio reikia, arba tam tikrą laiką, per kurį objektas įsibėgėja. Abu naudos laiko vienetus, tokius kaip sekundės, valandos ir kiti.
- Tarkime, automobilis, judantis 25 m/s greičiu (pradinis greitis), pradeda spartėti 3 m/s2 (pagreitis) 4 sekundes (laikas). Koks yra automobilio poslinkis po 4 sekundžių?

Žingsnis 2. Įveskite reikšmes į formulę
Skirtingai nuo ankstesnės formulės, čia pateikiamas tik pradinis greitis, todėl įsitikinkite, kad įvedėte teisingus duomenis.
Remiantis aukščiau pateiktais pavyzdiniais duomenimis, jūsų formulė atrodytų taip: S = 25 (4) + 1/2 (3) 4². Tai padeda pridėti skliaustelius aplink pagreičio dydį ir laiką, kad būtų galima atskirti skaičius
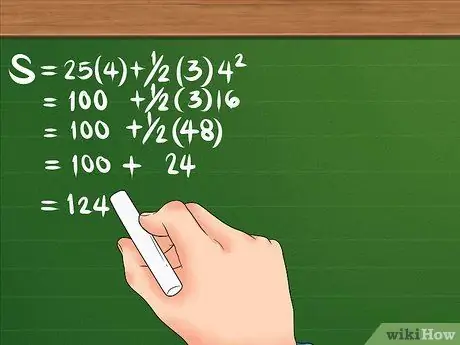
Žingsnis 3. Apskaičiuokite poslinkį, atlikdami tai teisinga veiksmų seka
Greitas būdas padėti prisiminti operacijų seką yra asilų tiltas Kur ir Kua ci Kadang Ba wa Juragan Turtles. Tai reiškia teisingą tvarką: skliaustelius, kvadratus, daugybą, padalijimą, sudėjimą ir atimtį.
Pažvelkime dar kartą į formulę: S = 25 (4) + 1/2 (3) 4². Pirma, 4 kvadratas, rezultatas yra 16. Tada padauginkite 16 iš 3, sudarydami 48; tada taip pat padauginkite 25 iš 4, kad gautumėte 100. Padalinkite 48 iš 2, kad gautumėte 24. Jūsų lygtis turėtų atrodyti taip: S = 100 + 24. Sudėjus abu kartu, poslinkis yra 124 metrai
4 dalis iš 5: Kampinio poslinkio apskaičiavimas

Žingsnis 1. Raskite kampinį poslinkį, kai objektas juda apskritimu
Nors jūs vis tiek skaičiuosite poslinkį naudodami tiesią liniją, turėsite rasti skirtumą tarp objekto pradžios ir pabaigos vietų, kai jis juda apskritimu.
- Įsivaizduokite merginą, sėdinčią karuselėje. Sukdamasis karuselėje jis judės apskrito tako. Kampinis poslinkis bando rasti trumpiausią atstumą tarp pradinės ir galutinės vietos, kai objektas nejuda tiesia linija.
- Kampinio poslinkio formulė yra tokia: = S/r, kur S yra tiesinis poslinkis, r yra spindulys ir yra kampinis poslinkis. Tiesinis poslinkis yra tai, kiek objektas juda išilgai lanko. Spindulys yra objekto atstumas iki apskritimo centro. Kampinis poslinkis yra vertė, kurią norime rasti.

Žingsnis 2. Įkiškite tiesinį poslinkį ir spindulį į lygtį
Atminkite, kad spindulys yra atstumas nuo apskritimo centro; kai kurios problemos parodys apskritimo skersmenį, kuris turi būti padalintas iš 2, kad rastumėte spindulį.
- Štai problemos pavyzdys: mergina važinėja karuselėmis. Sėdynė yra 1 metro atstumu nuo apskritimo centro (spindulio). Jei mergina juda lanko trajektorija 1,5 metro (tiesinis poslinkis), koks jos kampinis poslinkis?
- Jūsų lygtis atrodys taip: = 1,5/1.
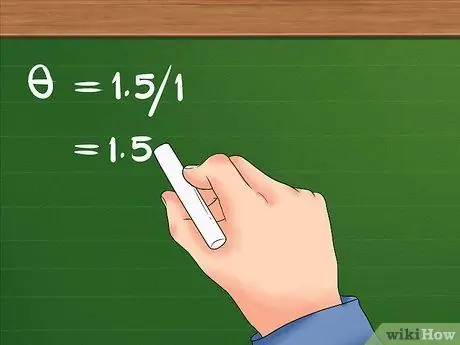
Žingsnis 3. Padalinkite linijinį poslinkį pagal spindulį
Šis padalijimas sukels objekto kampinį poslinkį.
- Padalinus 1,5 iš 1, rezultatas yra 1,5. Merginos kampinis poslinkis yra 1,5 radianai.
- Kadangi kampinis poslinkis matuoja, kiek objektas sukasi nuo pradinės padėties, jis turėtų būti matuojamas kaip kampas, o ne atstumas. Radianas yra vienetas, naudojamas kampams matuoti.
5 dalis iš 5: Supratimas apie migraciją
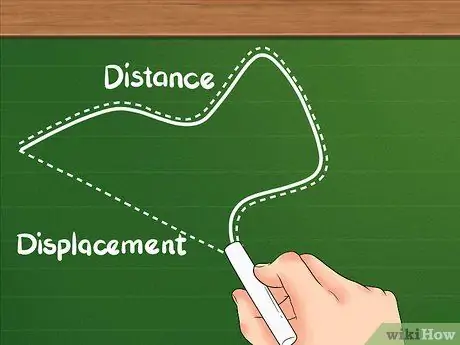
Žingsnis 1. Žinokite, kad atstumas skiriasi nuo poslinkio
Atstumas rodo, kiek toli nuvažiavo visą objektą.
- Atstumas dažnai vadinamas skaliariniu dydžiu. Atstumas rodo objekto nuvažiuotą atstumą, nepriklausomai nuo objekto krypties.
- Pavyzdžiui, jei einate 2 žingsnius į rytus, 2 žingsnius į pietus, 2 žingsnius į vakarus ir 2 žingsnius į šiaurę, grįšite į pradinę padėtį. Nors jūs išgyvenote visumą atstumas Tik už 10 žingsnių judėti Už 0 žingsnių, nes jūsų galutinė vieta yra ta pati, kaip ir jūsų pradinė vieta (jūsų kelias primena langelį).

Žingsnis 2. Supraskite, kad poslinkis yra skirtumas tarp dviejų vietų
Poslinkis nėra bendra judesio suma, kaip atstumas; pamainos sutelkia dėmesį į sritį tarp pradžios ir pabaigos vietų.
- Poslinkis vadinamas vektoriniu dydžiu ir parodo objekto padėties pasikeitimą, atsižvelgiant į objekto judėjimo kryptį.
- Pavyzdžiui, jūs einate į rytus 5 žingsnius. Jei 5 žingsnius grįšite į vakarus, judėsite priešinga kryptimi nei buvote. Nors įveikėte 10 žingsnių, jūsų padėtis nepasikeitė; jūsų poslinkis yra 0 žingsnių.

Žingsnis 3. Prisiminkite žodžius pirmyn ir atgal, kai bandote įsivaizduoti poslinkį
Judėjimas priešinga kryptimi pašalina objekto poslinkį.
Įsivaizduokite futbolo trenerį pirmyn ir atgal nuošalyje. Kai jis šaukė žaidėjus, jis kelis kartus pasislinko iš kairės į dešinę. Jei stebite, kaip jis juda iš kairės į dešinę, stebite bendrą jo nuvažiuotą atstumą. Tačiau tarkime, kad treneris sustoja pasikalbėti su gynėju nuošalyje. Jei jis prieš judėdamas yra kitoje vietoje nei jo pradinė vieta, jūs stebite trenerio judesį

Žingsnis 4. Žinokite, kad poslinkis matuojamas tiesiu, o ne apskritimu
Norėdami rasti poslinkį, turite rasti trumpiausią ir efektyviausią būdą apskaičiuoti skirtumą tarp dviejų taškų.
- Apskritas kelias nukels jus nuo pradinės vietos iki galutinės vietos, tačiau tai nėra trumpiausias kelias. Kad padėtumėte tai įsivaizduoti, įsivaizduokite, kad einate tiesia linija ir susiduriate su stulpu. Jūs negalite pralaužti šio stulpo, todėl apeinate jį. Nors jūsų galutinė pozicija yra tokia pati, kaip ir tada, kai pralaužėte stulpą, jums reikės papildomų veiksmų, kad pasiektumėte šį tikslą.
- Nors poslinkis yra tiesus kelias, žinokite, kad galite išmatuoti objekto poslinkį šiuo metu judėti apskritimu. Šis poslinkis vadinamas kampiniu poslinkiu ir gali būti apskaičiuotas suradus trumpiausią kelią nuo pradinės vietos iki galutinės vietos.

Žingsnis 5. Žinokite, kad poslinkis gali būti neigiamas, skirtingai nei atstumas
Jei jūsų galutinė vieta pasiekiama judant priešinga kryptimi nei jūsų pradinė kryptis, tada poslinkis yra neigiamas.
- Pavyzdžiui, einame 5 žingsnius į rytus ir 3 žingsnius į vakarus. Nors skaičiuodami judate 2 žingsnius nuo pradinės vietos, poslinkis yra -2, nes judate priešinga kryptimi. Jūsų atstumas visada bus teigiamas, nes negalite skaičiuoti atgal žingsniais, kilometrais ir pan.
- Neigiamas poslinkis nereiškia, kad poslinkis mažėja. Neigiamas tik reiškia, kad kryptis yra priešinga.

Žingsnis 6. Supraskite, kad kartais atstumas ir poslinkis gali būti vienodi
Jei eisite tiesiai 25 žingsnius ir sustosite, nuvažiuotas atstumas bus lygus poslinkiui nuo pradinės vietos.
- Tai taikoma tik judant iš vienos vietos iš pradinės vietos tiesia linija. Pavyzdžiui, jūs gyvenate San Franciske, Kalifornijoje, ir gaunate naują darbą Las Vegase, Nevadoje. Jei norite arti savo darbo, turite persikelti į Las Vegasą. Jei sėsite į skrendantį lėktuvą tiesiai iš San Francisko į Las Vegasą keliausite tą patį atstumą ir poslinkį x.
- Tačiau, jei važiuosite iš San Francisko į Las Vegasą, nuvažiuosite x atstumą, bet nuvažiuosite y. Kadangi vairuojant automobilį paprastai būna skirtingos kryptys (į rytus nuo šio kelio, į vakarus nuo to kelio), jūs keliausite ilgesnius atstumus nei trumpiausias atstumas tarp dviejų miestų.






