Kaip apskaičiuoti vidutinį greitį: 12 žingsnių (su nuotraukomis)

2024 Autorius: Jason Gerald | [email protected]. Paskutinį kartą keistas: 2024-02-01 14:14

Viskas, ko jums reikia norint apskaičiuoti vidutinį greitį, yra bendras poslinkis. arba padėties keitimas ir bendras laikas. Atminkite, kad greitis taip pat apskaičiuoja objekto kryptį ir greitį, todėl į savo atsakymą įtraukite kryptį, pvz., „Šiaurė“, „priekis“arba „kairė“. Jei jūsų greičio apskaičiavimo problema taip pat apima nuolatinį pagreitį, galite išmokti greitai rasti atsakymą dar lengviau.

Žingsnis

1 iš 2 metodas: vidutinio poslinkio greičio ir laiko apskaičiavimas

Žingsnis 1. Atminkite, kad greitis apima ir objekto greitį, ir kryptį

Greitis apibūdina greitį, kuriuo keičiasi objekto padėtis. Tai susiję ne tik su objekto judėjimo greičiu, bet ir su jo kryptimi. „100 metrų per sekundę į pietus“yra kitokia greičio vertė nei „100 metrų per sekundę į rytus“.

• Kiekiai, turintys kryptį, vadinami vektoriniais dydžiais “. Šį kiekį galima atskirti nuo besisukančio kiekio, vadinamo skaliariniu dydžiu, parašius rodyklę virš kintamojo. Pavyzdžiui, žymėjimas v reiškia normą, o žymėjimas v ^→ reiškia greitį arba greitį + kryptį. Šiame straipsnyje naudojamas žymėjimas v reiškia greitį.
• Mokslinių problemų atveju atstumui išreikšti turėtumėte naudoti skaitiklius ar kitus metrinius vienetus, o kasdieniams tikslams galite naudoti bet kurį jums patinkantį vienetą.

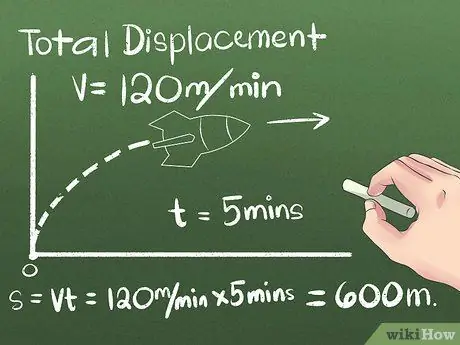
Žingsnis 2. Raskite bendrą poslinkio vertę

Poslinkis yra objekto padėties arba atstumo ir krypties tarp jo pradžios ir pabaigos taškų pokytis. Į objekto judėjimo kryptį prieš pasiekiant galutinę padėtį galima nepaisyti, nes atsižvelgiama tik į atstumą tarp pradžios ir pabaigos taškų. Pirmajame pavyzdyje naudosime objektą, judantį pastoviu greičiu viena kryptimi:

• Tarkime, kad raketa 5 minutes juda į šiaurę pastoviu 120 metrų per minutę greičiu. Norėdami apskaičiuoti galutinę padėtį, naudokite formulę s = vt arba naudokite praktinį mąstymą, kad apskaičiuotumėte raketos nuvažiuotą atstumą (5 minutės) (120 metrų per minutę) = 600 metrų į šiaurę nuo pradžios taško.
• Problemas, susijusias su nuolatiniu pagreičiu, galite jas išspręsti s = vt + at²arba naudokite trumpą metodą, aprašytą kitame skyriuje, kad rastumėte atsakymą.

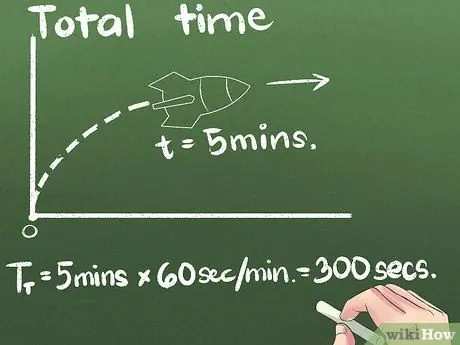
Žingsnis 3. Raskite visą praleistą laiką

Mūsų pavyzdyje raketa juda į priekį 5 minutes. Vidutinį greitį galite išreikšti bet kuriuo laiko vienetu, tačiau antrasis yra tarptautinis mokslinis standartinis vienetas. Šiame pavyzdyje pakeisime sekundžių vienetus: (5 minutės) x (60 sekundžių per minutę) = 300 sekundžių.

Net jei kyla mokslinių problemų, jei klausime naudojama valanda ar didesnis laiko vienetas, pirmiausia bus lengviau apskaičiuoti greitį, o tada galutinį atsakymą konvertuoti į metrus/sekundę

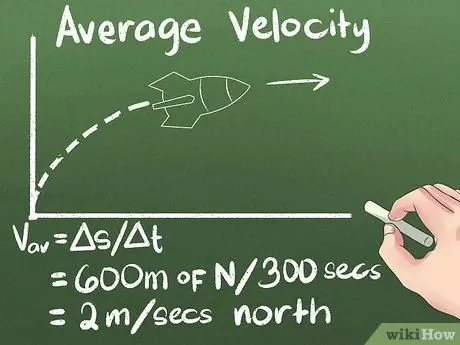
Žingsnis 4. Apskaičiuokite vidutinį greitį kaip poslinkį laikui bėgant

Jei žinote, kiek toli objektas juda ir kiek laiko užtruks, kad jį pasiektumėte, žinosite, kaip greitai jis juda. Taigi mūsų naudojamame pavyzdyje vidutinis raketos greitis yra (600 metrų į šiaurę) / (300 sekundžių) = 2 metrai per sekundę į šiaurę.

• Nepamirškite įtraukti krypties (pvz., „Priekio“arba „šiaurės“).
• Formulėje v_vid = s/Δt. Delta simbolis reiškia „pasikeitimas“, taigi s/Δt reiškia „padėties pasikeitimas per tam tikrą laikotarpį“.
• Vidutinis greitis gali būti parašytas kaip v_vid, arba kaip v su horizontalia linija virš jos.

Žingsnis 5. Išspręskite sudėtingesnes problemas

Jei objektas keičia savo kryptį ar greitį, nesusipainiokite. Vidutinis greitis vis dar „tik“apskaičiuojamas pagal bendrą poslinkį ir visą laiką. Tai, kas vyksta tarp pradžios ir pabaigos taškų, galite nepaisyti. Štai keletas objektų, keliaujančių tuo pačiu poslinkiu ir bendru laiku, taigi tuo pačiu vidutiniu greičiu, pavyzdžių:

• Anna 2 sekundes eina į vakarus 1 metro/s greičiu, tada staiga įsibėgėja iki 3 metrų per sekundę ir toliau 2 sekundes eina į vakarus. Bendras poslinkis yra (1 m/s į vakarus) (2 sek.) + (3 m/s į vakarus) (2 sek.) = 8 metrai į vakarus. Bendras laikas yra 2 sekundės + 2 sekundės = 4 sekundės. Taigi vidutinis greitis yra 8 metrai į vakarus/ 4 sekundės = 2 metrai per sekundę į vakarus.

• Bartas 3 sekundes eina į vakarus 5 m/s greičiu, tada apsisuka ir 1 sekundę eina į rytus 7 m/s greičiu. Mes galime galvoti apie judėjimą į rytus kaip „neigiamą judėjimą į vakarus“, todėl bendras poslinkis yra = (5 metrai/sek. Į vakarus) (3 sek.) + (-7 m/s į vakarus) (1 sek.) = 8 metrai. Bendras laikas = 4 sekundės. Vidutinis greitis = 8 metrai į vakarus / 4 sekundės = 2 metrai per sekundę į vakarus.

• Šarlotė ėjo į šiaurę 1 metrą, o paskui 8 metrus į vakarus, tada 1 metrą į pietus. Kelionės laikas yra 4 sekundės. Nubrėžkite diagramą ant popieriaus lapo ir pamatysite, kad galutinis taškas yra 8 metrai į vakarus nuo pradžios taško, taigi ši vertė yra poslinkis. Bendras laikas yra 4 sekundės, taigi vidutinis greitis yra 8 metrai į vakarus / 4 sekundės = 2 metrai per sekundę į vakarus.

  2 metodas iš 2: fiksuoto pagreičio vidutinio greičio apskaičiavimas

  

  Žingsnis 1. Apsvarstykite pradinį greitį ir pastovų pagreitį

  Tarkime, mūsų problema yra tokia: „Dviratis juda į dešinę 5 m/s greičiu, pastoviai įsibėgėdamas 2 m/s². Jei šis dviratis juda 5 sekundes, koks jo vidutinis greitis?"

  Jei vienetas „metras/sekundė²"Norėdami jus suklaidinti, parašykite jį kaip" metrai/sekundė/sekundė "arba" metrai per sekundę per sekundę. "2 metrų/sekundės/sekundės pagreitis reiškia, kad greitis didėja 2 metrais per sekundę.

  

  Žingsnis 2. Galutiniam greičiui rasti naudokite pagreitį

  Pagreitis, žymimas žymėjimu a, yra greičio (arba greičio) kitimo greitis. Greitis didėja pastoviu greičiu. Naudodami pagreitį galite piešti lentelę, kad rastumėte greitį skirtingu dviračio kelionės metu. Turime sukurti šią lentelę, kad surastume problemos galutinį tašką (t = 5 sekundės), tačiau sukursime ilgesnę lentelę, kad jums būtų lengviau suvokti šią sąvoką:

  • Pradiniame taške (laikas t = 0 sekundžių) dviratis juda 5 metrų/s greičiu.
  • Po 1 sekundės (t = 1) dviratis juda 5 metrų per sekundę greičiu + esant 5 metrų per sekundę + (2 metrai per sekundę)²) (1 sekundė) = 7 metrai per sekundę.
  • Kai t = 2, dviratis juda į dešinę 5+ (2) (2) = 9 metrų per sekundę greičiu.
  • Kai t = 3, dviratis juda į dešinę 5+ (2) (3) = 11 metrų per sekundę greičiu.
  • Kai t = 4, dviratis juda į dešinę 5+ (2) (4) = 13 metrų per sekundę greičiu.
  • Kai t = 5, dviratis juda į dešinę greičiu 5+ (2) (5) = 15 metrų per sekundę.

  

  Žingsnis 3. Naudokite šią formulę norėdami rasti vidutinį greitį

  Jei ir „tik“, jei pagreitis yra pastovus, vidutinis greitis bus lygus vidutinei galutinio ir pradinio greičio sumos vertei. (v_f +v_i)/2. Mūsų aukščiau pateiktos pavyzdinės problemos atveju pradinis dviračio greitis yra v_i 5 metrai per sekundę. Apskaičiavę galutinis greitis yra v_f 15 metrų per sekundę. Sudėjus šias dvi vertes, gauname (15 metrų per sekundę + 5 metrus per sekundę)/2 = (20 metrų per sekundę)/2 = 10 metrų per sekundę teisinga kryptimi.

  • Nepamirškite įtraukti krypties, šiuo atveju „teisingos“.
  • Šis terminas gali būti parašytas kaip v₀ (greitis momentu 0 arba pradinis greitis) ir v (galutinis greitis).

  

  Žingsnis 4. Intuityviai supraskite vidutinio greičio formulę

  Norėdami rasti vidutinį greitį, mes galime naudoti greitį bet kuriame taške ir rasti visų jų vidurkį. (Tai yra vidurkio apibrėžimas.) Kadangi tam reikia skaičiavimo ar begalinio laiko, supraskite šią formulę intuityviau. Užuot kiekvieną kartą skaičiavę, apskaičiuokite vidutinį dviejų laiko taškų greitį ir pamatykite rezultatus. Vienas momentas yra netoli važiavimo pradžios, kur dviratis važiuoja lėtai, o kitas - netoli galinio taško, kuriame dviratis važiuoja greitai.

  

  Žingsnis 5. Išbandykite intuityvią teoriją

  Naudokite aukščiau esančią lentelę, kad nustatytumėte greitį skirtingais laiko momentais. Kai kurios mūsų kriterijus atitinkančios poros yra (t = 0, t = 5), (t = 1, t = 4) arba (t = 2, t = 3). Jei norite, galite išbandyti šią formulę su t reikšmėmis, išskyrus sveikus skaičius.

  Nepriklausomai nuo pasirinktos taškų poros, vidutinis greitis tuo metu visada bus tas pats. Pavyzdžiui, ((5+15)/2), ((7+13)/2) arba ((9+11)/2) visi lygūs 10 metrų per sekundę į dešinę

  

  Žingsnis 6. Užbaikite intuityvų paaiškinimą

  Jei naudosime šį metodą su kiekvieno atlikto laiko sąrašu, toliau skaičiuosime pirmosios kelionės pusės ir antrosios kelionės pusės vidurkį. Laikas, per kurį įveikiama kiekviena pusė, yra vienodas, todėl baigus skaičiuoti neprarandamas joks greitis.

  • Kadangi bet kuri pora duos tą patį rezultatą, šių greičių vidurkis taip pat bus vienodas. Mūsų pavyzdyje visumos greitis yra „10 metrų per sekundę į dešinę“ir toliau bus 10 metrų per sekundę.
  • Šią vertę galime rasti apskaičiuodami bet kurios poros vidurkį, pavyzdžiui, pradinį ir galutinį greičius. Mūsų pavyzdyje šie greičiai pasiekiami esant t = 0 ir t = 5, ir juos galima apskaičiuoti naudojant aukščiau pateiktą formulę: (5+15)/2 = 10 metrų/sek.

  

  Žingsnis 7. Supraskite šią formulę matematiškai

  Jei jums labiau patinka įrodymai, užrašyti kaip formulės, galite pradėti nuo formulės, kad apskaičiuotumėte nuvažiuotą atstumą, laikydamiesi pastovaus pagreičio, ir iš čia gaukite formulę:

  • s = v_it + at². (Techniškai s ir t arba padėties pasikeitimas ir laiko pasikeitimas, bet jūs taip pat suprastumėte, jei parašytumėte s ir t.)
  • Vidutinis greitis v_vid apibrėžta kaip s/t, todėl įveskite formulę s/t pavidalu.
  • v_vid = s/t = v_i +
  • Pagreitis x laikas yra lygus viso greičio pokyčiui, arba v_f - v_i. Taigi formulėje galime pakeisti „at“ir gauti:
  • v_vid = v_i + (v_f - v_i).
  • Supaprastinti: v_vid = v_i + v_f - v_i = v_i + v_f = (v_f +v_i)/2.

  Patarimai

  • Greitis skiriasi nuo greičio, nes greitis yra vektorinis dydis, o greitis - skaliarinis dydis. Vektoriniai dydžiai apima ir kryptį, ir dydį, o skaliariniai dydžiai - tik dydį.
  • Jei objektas juda vienu matmeniu, pvz., Kairėn į dešinę, galite naudoti teigiamą skaičių, kad pavaizduotumėte vieną kryptį (pvz., Dešinę), o neigiamą skaičių-kitą kryptį (kairę). Parašykite šį užrašą puslapio viršuje, kad jis būtų aiškus žmonėms, skaitantiems jūsų darbą.