- Autorius Jason Gerald [email protected].
- Public 2024-01-16 19:43.
- Paskutinį kartą keistas 2025-01-23 12:26.
Tiriant optinius instrumentus, į objektyvą panašaus objekto „padidinimas“yra matomo vaizdo aukščio ir tikrojo objekto aukščio santykis. Pavyzdžiui, objektyvas, dėl kurio objektas gali atrodyti labai didelis, turi „didelį“didinimo koeficientą, o objektyvas, dėl kurio objektas atrodo mažas, turi „mažą“didinimo koeficientą. Objekto padidinimo formulė paprastai apskaičiuojama naudojant formulę M = (hi/ho) = -(di/do), kur M = padidinimas, hi = vaizdo aukštis, ho = objekto aukštis ir di ir D.o = vaizdo ir objekto atstumas.
Žingsnis
1 metodas iš 2: Vieno objektyvo padidinimo apskaičiavimas
Pastabos: A. susiliejantis objektyvas platesnis centre nei kraštuose (kaip padidinamasis stiklas). a skirtingas objektyvas platesnis kraštuose nei centre (kaip dubuo). Abiejų lęšių padidinimo apskaičiavimas yra tas pats, naudojant viena svarbi išimtis. Spustelėkite čia, jei norite tiesiogiai pereiti prie skirtingų objektyvų išimčių.
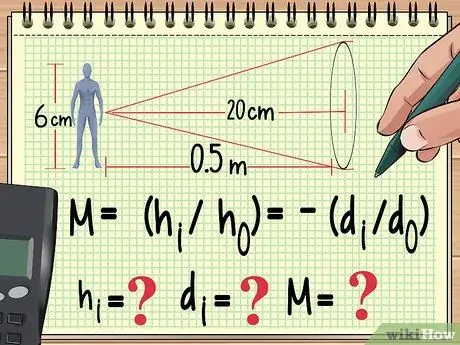
Žingsnis 1. Pradėkite nuo savo lygties ir kintamųjų, kuriuos jau žinote
Kaip ir bet kuri kita fizikos problema, išsiplėtimo problemos sprendimas yra užrašyti lygtį, kurią naudosite ją apskaičiuodami. Iš čia galite dirbti atgal, kad surastumėte kintamojo, kurio neradote, vertę naudodami naudojamą lygtį.
-
Pavyzdžiui, tarkime, kad 6 cm aukščio lėlė yra padėta vieno metro atstumu nuo a susiliejantis objektyvas kurių židinio nuotolis 20 cm. Jei norime apskaičiuoti padidinimą, vaizdo aukštį ir vaizdo atstumą, galime pradėti rašyti savo lygtį taip:
-
- M = (hi/ho) = -(di/do)
-
- Dabar mes žinome, ho (lėlės aukštis) ir do (lėlės atstumas nuo objektyvo). Mes taip pat žinome objektyvo židinio nuotolį, kurio šioje lygtyje nėra. Mes suskaičiuosime hi, diir M..

Žingsnis 2. Naudodami objektyvo lygtį, kad gautumėte di.
Jei žinote atstumą nuo didinamo objekto ir objektyvo židinio nuotolį, apskaičiuoti atstumą nuo susidariusio vaizdo yra labai paprasta naudojant objektyvo lygtį. Objektyvo lygtis yra 1/f = 1/do + 1/di, kur f = objektyvo židinio nuotolis.
-
Šioje problemos pavyzdyje mes galime naudoti objektyvo lygtį apskaičiuoti di. Įveskite f ir d reikšmesi tada išspręskite lygtį:
-
- 1/f = 1/do + 1/di
- 1/20 = 1/50 + 1/di
- 5/100 - 2/100 = 1/di
- 3/100 = 1/di
- 100/3 = di = 33,3 cm
-
- Objektyvo židinio nuotolis yra atstumas nuo objektyvo centro iki taško, kuriame židinio taškas perduoda šviesą. Jei kada nors šviesą su padidinamuoju stiklu sutelkėte į degančias skruzdėles, tai matėte. Pamokos klausimuose paprastai nurodomas šio taško dydis. Realiame gyvenime šios specifikacijos paprastai užrašomos ant etiketės, esančios ant objektyvo.

Žingsnis 3. Apskaičiuojant hi.
Apskaičiavus do ir D.i, galite apskaičiuoti padidinto objekto aukštį ir objektyvo padidinimą. Atkreipkite dėmesį į du lygybės ženklus lęšio didinimo lygtyje (M = (hi/ho) = -(di/do)) - tai reiškia, kad visos šios lygties dalys yra lygios viena kitai, todėl galime apskaičiuoti M ir hi kokia tvarka norime.
-
Šios problemos pavyzdyje galime apskaičiuoti hi kaip šitas:
-
- (hi/ho) = -(di/do)
- (hi/6) = -(33, 3/50)
- hi = -(33, 3/50) x 6
- hi = - 3, 996 cm
-
- Atminkite, kad objekto aukštis čia yra neigiamas, o tai rodo, kad vaizdas, kurį pamatysime vėliau, bus apverstas (viršuje-apačioje).

Žingsnis 4. M. apskaičiavimas
Paskutinį kintamąjį galite apskaičiuoti pagal lygtį -(di/do) arba (hi/ho).
-
Šiame pavyzdyje M apskaičiavimas yra toks:
-
- M = (hi/ho)
- M = (-3, 996/6) = - 0, 666
-
-
Rezultatas taip pat bus tas pats, kai jis apskaičiuojamas naudojant d reikšmę:
-
- M = -(di/do)
- M = -(33, 3/50) = - 0, 666
-
- Atminkite, kad priartinimas neturi vieneto etiketės.
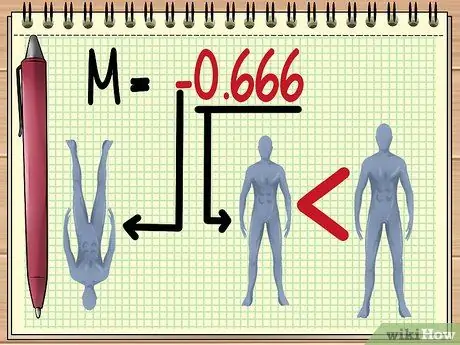
Žingsnis 5. M reikšmės supratimas
Gavę M vertės dydį, galite įvertinti kelis dalykus apie vaizdą, kurį matysite per objektyvą, būtent:
-
Dydis.
Kuo didesnė „absoliuti M vertė“, tuo didesnis objektyvas bus matomas. M reikšmė nuo 0 iki 1 rodo, kad objektas atrodys mažesnis.
-
Objekto orientacija.
Neigiama reikšmė rodo, kad susidaręs vaizdas bus apverstas.
- Čia pateiktame pavyzdyje M reikšmė -0,666 reiškia, kad pagal esamo kintamojo reikšmę bus matomas lėlės šešėlis. aukštyn kojomis ir dviem trečdaliais mažesnis už tikrąjį dydį.
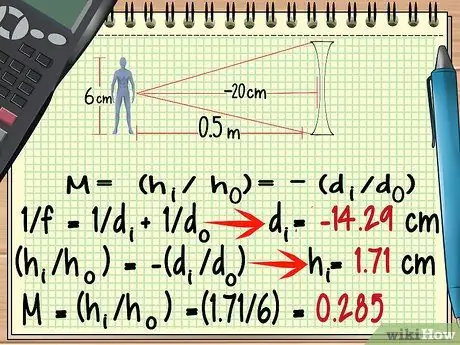
Žingsnis 6. Jei skiriasi objektyvas, naudokite neigiamą židinio tašką
Nors besikeičiančio objektyvo forma labai skiriasi nuo susiliejančio lęšio formos, jo padidinimą galite apskaičiuoti pagal tą pačią formulę, kaip nurodyta aukščiau. Išimtys, į kurias reikia atsižvelgti, yra Skirtingo objektyvo židinio taškas yra neigiamas.
Aukščiau pateiktame pavyzdiniame uždavinyje tai paveiks atsakymą, kurį gausite apskaičiuodami di, todėl būtinai atkreipkite į tai dėmesį.
-
Pakartokime aukščiau pateiktą pavyzdinę problemą, tik dabar mes naudojame skirtingą židinio nuotolio objektyvą - 20 cm.
Kiti kintamieji išlieka tos pačios vertės.
-
Pirmiausia apskaičiuosime di naudojant objektyvo lygtį:
-
- 1/f = 1/do + 1/di
- 1/-20 = 1/50 + 1/di
- -5/100 - 2/100 = 1/di
- -7/100 = 1/di
- -100/7 = di = - 14, 29 cm
-
-
Dabar mes apskaičiuosime hi ir M, kurio reikšmė di naują.
-
- (hi/ho) = -(di/do)
- (hi/6) = -(-14, 29/50)
- hi = -(-14, 29/50) x 6
- hi = 1, 71 cm
- M = (hi/ho)
- M = (1, 71/6) = 0, 285
-
2 metodas iš 2: kelių lęšių padidinimo apskaičiavimas
Paprastas dviejų objektyvų metodas
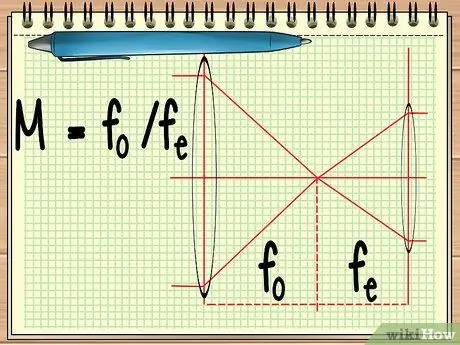
Žingsnis 1. Apskaičiuokite dviejų objektyvų židinio tašką
Kai naudojate instrumentą, kurį sudaro du vienas šalia kito išdėstyti lęšiai (pvz., Teleskopas ar žiūronas), tereikia išsiaiškinti dviejų objektyvų židinio tašką, kad būtų galima apskaičiuoti bendrą dviejų lęšių padidinimą. tai galima apskaičiuoti paprasta lygtimi M = fofe.
Lygybėje fo yra objektyvo židinio taškas ir fe yra okuliaro židinio taškas. Objektyvus objektyvas yra didelis objektyvas, esantis arti objekto, o akies lęšis yra objektyvas, esantis netoli stebėtojo akies.

Žingsnis 2. Įjunkite turimą informaciją į lygtį M = fofe.
Kai turite abiejų lęšių židinio taškus, juos labai lengva apskaičiuoti, - apskaičiuokite santykį, objektyvo objektyvo židinio nuotolį padaliję iš okuliaro židinio nuotolio. Gautas atsakymas yra bendras įrankio padidinimas.
-
Pavyzdžiui, tarkime, kad paprastas teleskopas, parašyta, kad objektyvo židinio taškas yra 10 cm, o okuliaro židinio taškas yra 5 cm, tada padidinimas yra 10/5 = 2.
Sudėtingas metodas
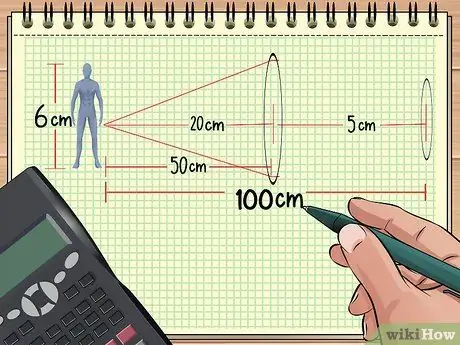
Žingsnis 1. Apskaičiuokite atstumą tarp lęšių ir objekto
Jei turite du objektyvus, išdėstytus iš eilės priešais objektą, bendrą padidinimą galima apskaičiuoti, jei žinote atstumą nuo lęšių iki objekto, objekto dydį ir dviejų objektyvų židinio tašką. Likusią dalį taip pat galima apskaičiuoti.
Pvz., Tarkime, kad mes sutvarkome objektus ir lęšius, kaip aprašyta 1 pavyzdyje: lėlė yra 50 cm atstumu nuo susiliejančio lęšio, kurio židinio nuotolis yra 20 cm. Dabar padėkite antrąjį objektyvą, kurio židinio taškas yra 5 cm, 50 cm atstumu nuo pirmojo lęšio (100 cm nuo lėlės.) Po to mes apskaičiuosime bendrą padidinimą, naudodami gautą informaciją
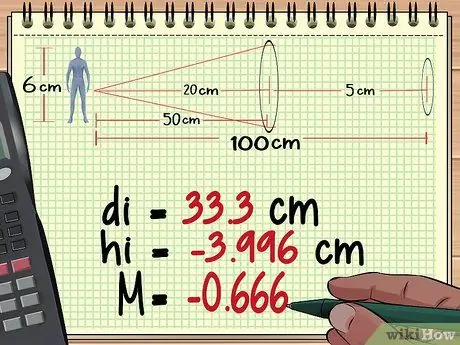
2 žingsnis. Apskaičiuokite objekto atstumą, aukštį ir padidinimą iš 1 objektyvo
Pirmoji kelių lęšių padidinimo skaičiavimo dalis yra tokia pati kaip vieno objektyvo padidinimo apskaičiavimas. Pradėkite nuo objektyvo, esančio arčiausiai objekto, naudokite objektyvo lygtį, kad surastumėte atstumą nuo suformuoto vaizdo, tada naudokite didinimo lygtį, kad surastumėte vaizdo aukštį ir padidinimą. Spustelėkite čia, jei norite peržiūrėti daugiau vieno objektyvo padidinimo skaičiavimų.
-
Remdamiesi 1 metodo skaičiavimais, nustatome, kad pirmasis objektyvas sukuria tokį aukštą vaizdą - 3, 996 cm, atstumas 33,3 cm už objektyvo ir padidinus - 0, 666.
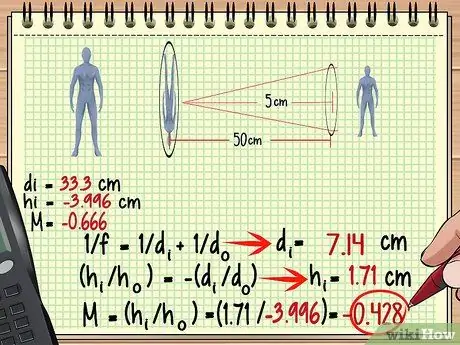
Žingsnis 3. Naudokite pirmojo objektyvo vaizdą kaip objektą iš antrojo objektyvo
Dabar labai lengva rasti antrojo objektyvo padidinimą, aukštį ir daugiau - tiesiog naudokite tą patį metodą, kurį naudojote pirmam objektyvui, tik šį kartą vaizdą laikykite objektu. Atminkite, kad vaizdo atstumas iki antrojo objektyvo ne visada sutampa su objekto atstumu iki pirmojo objektyvo.
-
Aukščiau pateiktame pavyzdyje, kadangi vaizdas susidaro 33,3 cm už pirmojo objektyvo, atstumas yra 50-33,3 = 16,7 cm priešais antrąjį objektyvą. Panaudokime šį matavimą ir antrojo objektyvo židinio nuotolį, kad surastume antrojo objektyvo suformuotą vaizdą.
-
- 1/f = 1/do + 1/di
- 1/5 = 1/16, 7 + 1/di
- 0, 2 - 0, 0599 = 1/di
- 0, 14 = 1/di
- di = 7, 14 cm
-
-
Dabar galime apskaičiuoti hi ir M - antrasis objektyvas:
-
- (hi/ho) = -(di/do)
- (hi/-3, 996) = -(7, 14/16, 7)
- hi = -(0, 427) x -3, 996
- hi = 1, 71 cm
- M = (hi/ho)
- M = (1, 71/-3, 996) = - 0, 428
-
Žingsnis 4. Toliau skaičiuokite papildomus objektyvus
Šis pagrindinis požiūris yra tas pats, jei prieš objektą yra trys, keturi ar šimtai lęšių. Kiekvieno objektyvo atveju laikykite ankstesnio objektyvo vaizdą objektu ir naudokite objektyvo lygtį bei padidinimo lygtį norimam atsakymui rasti.
Atminkite, kad kiekvienas paskesnis objektyvas gali nuolat apversti susidariusį vaizdą. Pavyzdžiui, padidinimo vertė, kurią gavome anksčiau (-0, 428), rodo, kad vaizdas, kurį matysime, yra maždaug 4/10 tikrojo objekto dydžio, bet statmenas, nes vaizdas iš ankstesnio objektyvo yra apverstas
Patarimai
- Žiūronai paprastai pateikia didinimo specifikacijų paaiškinimą skaičiaus ir kito skaičiaus pavidalu. Pavyzdžiui, žiūronai gali būti nurodyti kaip 8x25 arba 8x40. Kai taip parašyta, pirmasis skaičius yra žiūronų padidinimas. Nesvarbu, net jei pateiktame pavyzdyje abu skaičiai yra skirtingo dydžio, abu žiūronai padidinami 8 kartus. Antrasis skaičius rodo, koks aiškus vaizdas bus suformuotas žiūronais.
- Atminkite, kad vieno lęšio lupos padidinimas bus neigiamas, jei objekto atstumas yra didesnis nei objektyvo židinio nuotolis. Tai nereiškia, kad susidaręs vaizdas bus mažesnis. Tokiu atveju padidėjimas vis tiek vyksta, tačiau susidaręs vaizdas stebėtojas matys aukštyn kojomis (iš viršaus į apačią).






