- Autorius Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-19 22:13.
- Paskutinį kartą keistas 2025-06-01 06:07.
Atimtis yra tiesiog atimti vieną skaičių iš kito. Nesunku atimti vieną sveiką skaičių iš kito, tačiau atimti gali būti sudėtinga, jei atimate trupmenas ar dešimtainius skaičius. Kai suprasite atimtį, galėsite naudoti sudėtingesnes matematikos sąvokas ir lengviau sudėti, dauginti ir padalyti skaičius.
Žingsnis
1 metodas iš 6: didelių sumų atėmimas skolinantis

Žingsnis 1. Užsirašykite didelį skaičių
Pavyzdžiui, norite išspręsti 32 - 17. Pirmiausia užsirašykite 32.

2 žingsnis. Po juo parašykite mažesnį skaičių
Įsitikinkite, kad dešimčių ir vienetų reikšmės dedamos į teisingus stulpelius, kad 3 iš 32 būtų tiesiai virš 1 iš 17, o 2 iš 32 - tiesiai virš 7 iš 17.
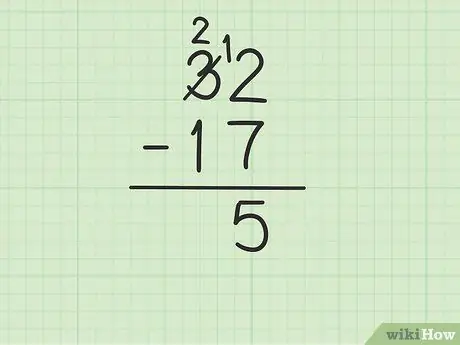
Žingsnis 3. Atimkite viršutinį skaičių vienetų stulpelyje iš skaičiaus apačioje
Tačiau tai gali būti sudėtinga, jei apatinis skaičius yra didesnis nei viršutinis. Šiuo atveju 7 yra didesnis nei 2. Štai ką turite padaryti:
- Norėdami paversti 2 į 12, turite skolintis iš skaičiaus 3 iš 32 (taip pat žinomas kaip grupavimas).
- Perbraukite skaičių 3 iš 32 ir pakeiskite jį skaičiumi 2, o skaičius 2 tampa 12.
- Dabar galite atimti 12 - 7, kuris lygus 5. Po dviem atimamais skaičiais parašykite 5 taip, kad jie būtų naujos eilutės vienetų stulpelyje.
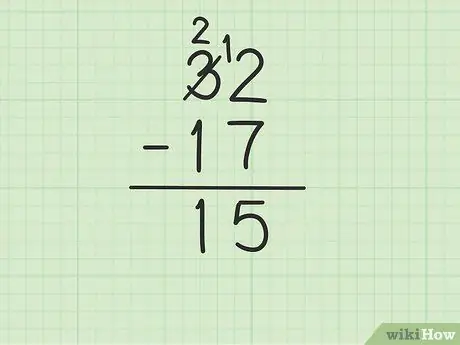
Žingsnis 4. Iš apatinio skaičiaus atimkite viršutinį skaičių dešimčių stulpelyje
Prisiminkite, kad 3 tapo 2. Dabar atimkite 1 iš 17 iš 2, kad gautumėte (2-1) 1. Rašykite 1 žemiau, dešimčių stulpelyje, į kairę nuo 5 vienetų stulpelyje. Jūs rašote 15. Tai yra, 32 - 17 = 15.
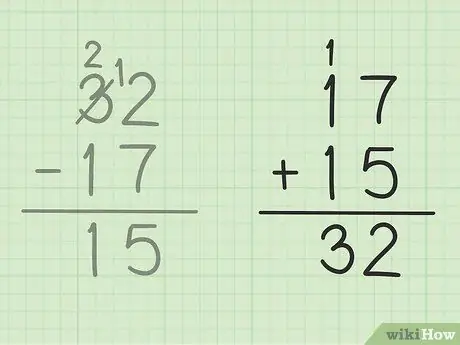
Žingsnis 5. Patikrinkite savo darbą
Jei norite įsitikinti, kad teisingai atėmėte du skaičius, jums tereikia pridėti atsakymą prie mažesnio skaičiaus, kad gautumėte didelį skaičių. Į šią problemą turite įtraukti savo atsakymą, 15 prie mažesnio atimties skaičiaus, 17. 15 + 17 = 32, kad atsakymas būtų teisingas. Saugu!
2 metodas iš 6: atimkite mažus sveikus skaičius
Žingsnis 1. Raskite didesnį skaičių
Tokios problemos kaip 15-9 turės kitokį būdą nei 2-30.
- 15-9 klausimų pirmasis skaičius 15 yra didesnis nei antrasis skaičius 9.
- 2-30 klausimuose antrasis skaičius 30 yra didesnis už pirmąjį, 2.
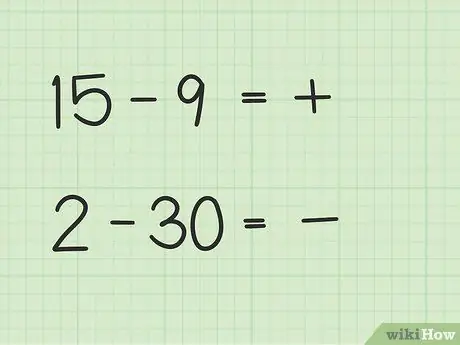
Žingsnis 2. Nuspręskite, ar jūsų atsakymas bus teigiamas, ar neigiamas
Jei pirmasis skaičius yra didesnis, atsakymas yra teigiamas. Jei antrasis skaičius yra didesnis, atsakymas yra neigiamas.
- Į pirmąjį klausimą, 15 - 9, jūsų atsakymas yra teigiamas, nes pirmasis skaičius yra didesnis nei antrasis.
- Į antrąjį klausimą, 2-30, jūsų atsakymas yra neigiamas, nes antrasis skaičius yra didesnis nei pirmasis.
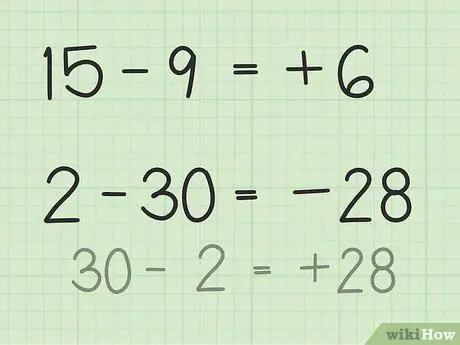
Žingsnis 3. Raskite dviejų skaičių skirtumą
Norėdami atimti du skaičius, turite įsivaizduoti skirtumą tarp dviejų skaičių ir apskaičiuoti skaičius tarp jų.
- 15-9 klausimams įsivaizduokite 15 pokerio žetonų krūvą. Išmeskite 9 žetonus ir tik 6. Taigi, 15 - 9 = 6. Taip pat galite įsivaizduoti skaičių eilutę. Pagalvokite apie skaičius nuo 1 iki 15, tada išmeskite arba grąžinkite 9 vienetus, kad gautumėte 6.
- 2-30 klausimų atveju lengviausia tai išspręsti apverčiant skaičių ir atėmus rezultatą padaryti neigiamą. Taigi, 30 - 2 = 28, taigi 28 ir 30 turi skirtumą 2. Dabar padarykite rezultatą neigiamą, nes jau nustatėte, kad atsakymas yra neigiamas, nes antrasis skaičius yra didesnis nei pirmasis. Taigi, 2-30 = -28.
3 metodas iš 6: dešimtainių skaičių atėmimas
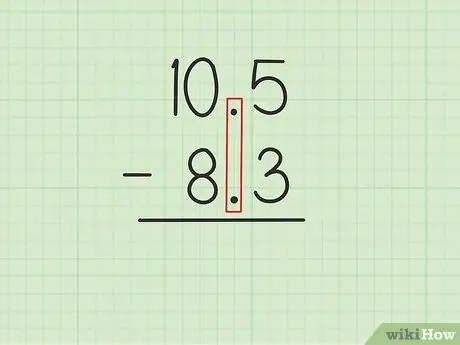
Žingsnis 1. Užrašykite didesnį skaičių per mažesnį skaičių su dešimtainiais taškais
Tarkime, norite išspręsti šias problemas: 10, 5 - 8, 3. Parašykite 10, 5 per 8, 3 taip, kad dviejų skaičių dešimtainiai taškai būtų lygiagrečiai., 5 iš 10, 5 turi būti tiesiai virš, 3 iš 8, 3 ir 0 iš 10, 5 turi būti aukščiau 8 iš 8, 3.
Jei turite problemų, nes du skaičiai po kablelio neturi vienodo skaičiaus, tuščioje vietoje rašykite 0, kol skaičių suma bus vienoda. Pavyzdžiui, problema yra 5, 32 - 4, 2, galite ją parašyti kaip 5, 32 - 4, 2 0. Tai nepakeis antrojo skaičiaus vertės, tačiau palengvins dviejų skaičių atėmimą.

Žingsnis 2. Atimkite viršutinį skaičių dešimčių stulpelyje iš žemiau pateikto skaičiaus
Tokiu atveju jūs turite atimti 3 iš 5. 5 - 3 = 2, taigi jūs turite parašyti 2 pagal 3 iš 8, 3.
Įsitikinkite, kad atsakyme įrašėte dešimtainį tašką, kad jis būtų parašytas, 2

Žingsnis 3. Atimkite skaičių, esantį virš vienetų stulpelio, iš po jo esančio skaičiaus
Turite atimti 8 iš 0. Pasiskolinkite 1 iš dešimčių dalies, kad pakeistumėte 0 į 10, ir atimkite 10 - 8, kad gautumėte 2. Taip pat galite neskaičiuojant 10 - 8 skaičiuoti, nes antro dešimties stulpelyje nėra skaičių. Atsakymą parašykite po 8, kairėje po kablelio.

Žingsnis 4. Užsirašykite savo galutinį rezultatą
Galutinis rezultatas yra 2, 2.

Žingsnis 5. Patikrinkite savo darbą
Jei norite įsitikinti, kad dešimtainis atėmimas yra teisingas, jums tereikia pridėti atsakymą prie mažesnio skaičiaus, kad gautumėte didesnį skaičių. 2, 2 + 8, 3 = 10, 5, taigi jūs baigėte.
4 metodas iš 6: atimkite trupmenas

Žingsnis 1. Sulygiuokite trupmenos vardiklį ir skaitiklį
Tarkime, kad norite išspręsti problemas 13/10 - 3/5. Užrašykite užduotį taip, kad du skaitikliai - 13 ir 3 bei du vardikliai - 10 ir 5 būtų vienas priešais kitą. Šie du skaičiai yra atskirti atimties ženklu. Tai padės lengviau įsivaizduoti problemą ir ją išspręsti.

Žingsnis 2. Raskite mažiausią bendrą vardiklį
Mažiausias bendras vardiklis yra mažiausias skaičius, kurį galima padalyti iš dviejų skaičių. Šiame pavyzdyje turite rasti mažiausią bendrą vardiklį, kuris dalijasi iš 10 ir 5. Pamatysite, kad 10 yra mažiausias abiejų skaičių bendras vardiklis, nes 10 dalijasi iš 10 ir 5.
Atminkite, kad mažiausias bendras dviejų skaičių vardiklis ne visada yra vienas iš jų. Pavyzdžiui, mažiausias bendras 3 ir 2 vardiklis yra 6, nes 6 yra mažiausias skaičius, kurį galima padalyti iš dviejų skaičių
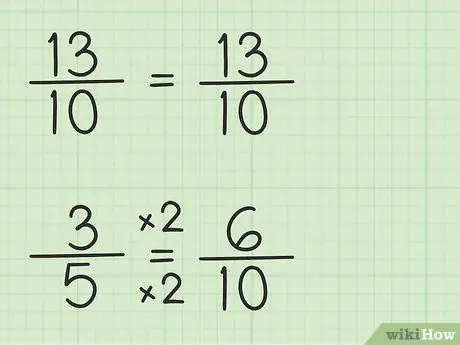
Žingsnis 3. Užrašykite trupmenas naudodami tą patį vardiklį
Skaičius 13/10 gali būti parašytas taip pat, nes vardiklis yra 10, mažiausias bendras vardiklis, kuris yra 10, kartų 1. Tačiau trupmeną 3/5 reikia perrašyti, nes vardiklis yra 5, mažiausias bendras vardiklis, o tai yra 10, kartų 2. Taigi trupmeną 3/5 reikia padauginti iš 2/2, kad gautume vardiklį 10, taigi 3/5 x 2/2 = 6/10. Radote lygiavertę trupmeną. 3/5 yra lygus 6/10, nors 6/10 leidžia atimti pirmąjį skaičių, 13/10.
Parašykite naują klausimą: 13/10 - 6/10
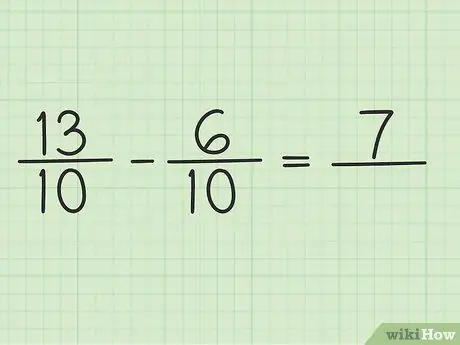
Žingsnis 4. Atimkite skaitiklį iš dviejų skaičių
Tiesiog atimkite 13 - 6, taigi rezultatas yra 7. Jūs negalite pakeisti trupmenos vardiklio.
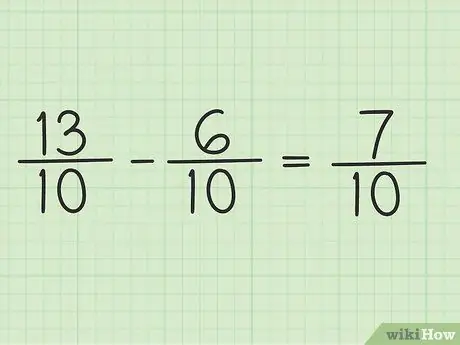
Žingsnis 5. Parašykite naują skaitiklį per tą patį vardiklį, kad gautumėte galutinį rezultatą
Naujasis skaitiklis yra 7. Abiejų trupmenų vardiklis yra 10. Jūsų galutinis rezultatas yra 7/10.
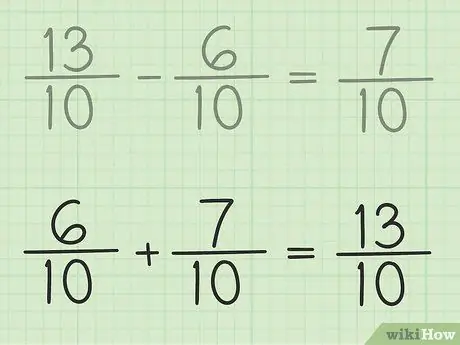
Žingsnis 6. Patikrinkite savo darbą
Jei norite įsitikinti, kad trupmeną atimate, tiesiog pridėkite savo atsakymą ir mažesnę trupmeną, kad rezultatas būtų didesnis. 7/10 + 6/10 = 13/10. Tai pabaigta.
5 iš 6 metodas: trupmenų atėmimas iš sveikų skaičių

1 žingsnis. Užsirašykite problemą
Pavyzdžiui, tarkime, kad norite išspręsti šią problemą: 5 -. Užsirašykite.
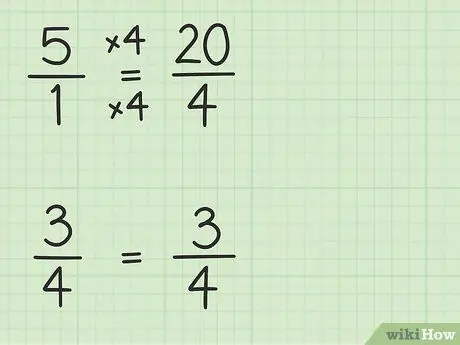
Žingsnis 2. Konvertuokite sveikus skaičius į trupmenas, turinčias tą patį vardiklį kaip ir kitos trupmenos
Jei norite atimti du skaičius, 5 konvertuosite į trupmeną, kurios vardiklis yra 4. Taigi jūs turite galvoti apie 5 kaip 5/1 dalį. Tada galite padauginti naujos trupmenos skaitiklį ir vardiklį iš 4, kad abu skaičių vardikliai taptų vienodi. Taigi 5/1 x 4/4 = 20/4. Ši dalis lygi 5, tačiau leidžia atimti du skaičius.
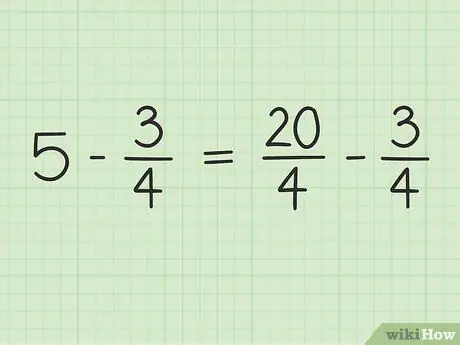
Žingsnis 3. Perrašykite problemą
Naują problemą galima parašyti taip: 20/4 - 3/4.
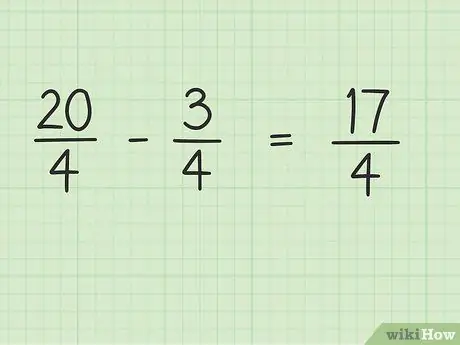
Žingsnis 4. Atimkite trupmenos skaitiklį, o vardiklis išlieka tas pats
Dabar tiesiog atimkite 20 iš 3, kad gautumėte galutinį rezultatą. 20 - 3 = 17, taigi 17 yra naujas skaitiklis. Vardiklį galite palikti tą patį.
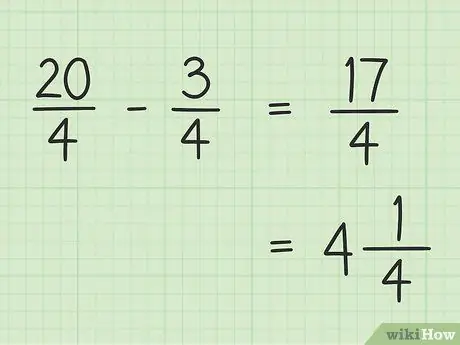
Žingsnis 5. Užsirašykite savo galutinį rezultatą
Galutinis rezultatas yra 17/4. Jei norite parašyti kaip mišrų skaičių, padalinkite 17 iš 4, kad rezultatas būtų 4, o likusi dalis - 1, kad galutinis 17/4 būtų lygus 4.
6 metodas iš 6: kintamųjų atėmimas
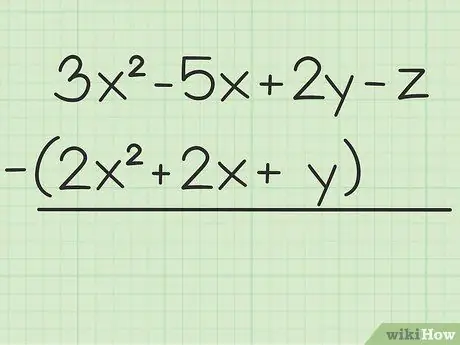
Žingsnis 1. Užsirašykite problemą, kurią norite išspręsti
Pavyzdžiui, toks klausimas: 3x2 - 5x + 2y - z - (2x2 + 2x + y). Parašykite pirmąjį kintamųjų rinkinį per antrąjį.
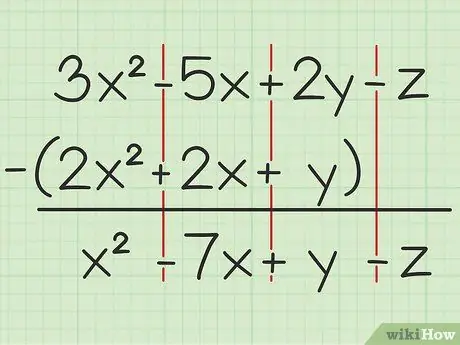
Žingsnis 2. Atimkite tuos pačius kintamuosius
Jei susiduriate su kintamuoju, galite pridėti arba atimti tik tą patį kintamąjį, kuris parašytas tuo pačiu kvadrato laipsniu. Tai reiškia, kad galite atimti 4 kartus2 nuo 7x2, bet negali atimti 4x iš 4y. Taigi, galite išspręsti problemą taip:
- 3 kartus2 - 2x2 = x2
- -5x -2x = -7x
- 2y - y = y
- -z -0 = -z
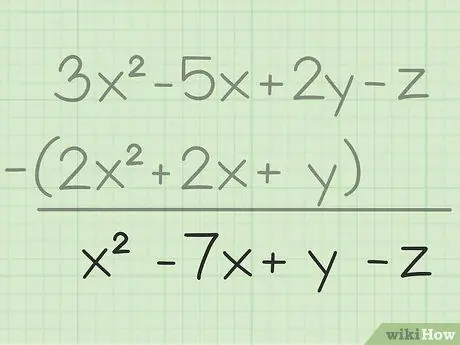
Žingsnis 3. Užsirašykite galutinį rezultatą
Jūs atėmėte visus tuos pačius kintamuosius, jums tereikia parašyti galutinį rezultatą, kuriame bus visi jūsų atimti kintamieji. Štai galutinis rezultatas:






